Penjelasan Matriks juga bisa melalui video di bawah ini !
Assalamu’alaikum Wr. Wb.
Selamat datang di Visi Pendidikan Generasi Emas 2045, terima kasih telah berkenan mampir di website saya generasiemas2045.com. Semoga Allah SWT senantiasa memberi kita kesehatan, keselamatan, perlindungan, kemudahan segala urusan dan rejeki untuk kita semua dan keluarga yang kita sayangi. Sholawat serta salam tidak lupa kita sampaikan pada beliau Nabi Muhammad SAW yang telah menuntun umat manusia dari zaman kegelapan menuju masyarakat yang tercerahkan. Pada kesempatan kali ini, saya upload materi matematika dengan peta materi sebagai berikut :
DAFTAR ISI
Aplikasi Matriks di Dunia Nyata 
Penjumlahan dan Pengurangan Matriks 
Invers, Determinan dan Adjoin Matriks 
MATRIKS
Tujuan
Spesifikasi kinerja yang diharapkan dikuasai siswa setelah mengikuti seluruh kegiatan belajar adalah siswa dapat:
- membuat susunan bilangan dalam bentuk Matriks
- menyebutkan ordo suatu Matriks
- menuliskan bentuk umum suatu Matriks dalam ordo tertentu
- mengidentifikasi jenis-jenis Matriks
- menyelesaikan kesamaan Matriks
- menjumlahkan atau mengurangkan dua Matriks atau lebih
- mengalikan skolar dengan Matriks
Uraian Materi
Pengertian Matriks 
Dalam kehidupan sehari-hari dan dalam matematika, berbagai keterangan seringkali disajikan dalam bentuk matriks.
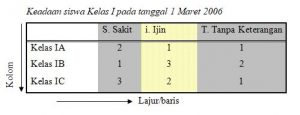
Contoh 1:
Contoh 2.
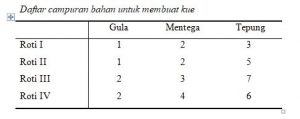
Apabila dari daftar tabel contoh 1 dan 2 tersebut kepala kolom dan baris dihilangkan, kemudian susunan lambang bilangan itu diberi tanda kurung atau kurung siku, maka susunan itu disebut matriks.

Jadi Matriks adalah suatu susunan bilangan-bilangan yang berbentuk persegi atau persegi panjang yang diatur pada baris dan kolom dan diletakkan di dalam dua kurung biasa atau kurung siku.
Bentuk umum matriks:

Notasi Matriks 
Suatu matriks dinyatakan dengan sebuah huruf capital.
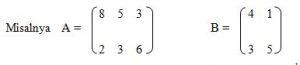
Ordo Matriks 
Ordo suatu matriks ditentukan oleh banyaknya baris diikuti banyaknya kolom.
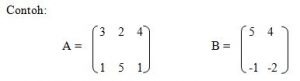
matriks A mempunyai 2 baris dan 3 kolom, maka dikatakan ordonya 2 x 3 (dibaca “2 kali 3”) dan ditulis A(2 x 3).
Matriks B mempunyai 2 baris dan 2 kolom, karena banyaknya baris sama dengan banyaknya kolom, maka matriks B disebut matriks bujur sangkar. Karena istilah bujur sangkar disesuaikan menjadi persegi, maka disebut juga sebagai matriks persegi. Maka matriks B adalah matriks persegi dengan ordo 2.
Macam-macam Matriks 
Matriks baris
Matriks yang hanya mempunyai elemen satu baris.

Matriks kolom (lajur)
Matriks yang hanya mempunyai elemen satu kolom.
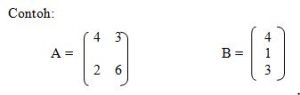
Matriks Bujur Sangkar (Persegi)
Matriks yang banyaknya baris sama dengan banyaknya kolom.

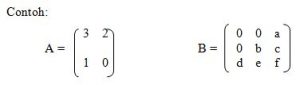
Matriks Segitiga
Matriks persegi yang dipisahkan oleh diagonal, dengan elemen-elemen 0 pada separuh bagiannya.
Kesamaan Matriks 
Dua matriks A dan B dikatakan sama jika:
- Ordonya sama dan
- Elemen-elemen yang siletak (bersesuaian) sama.
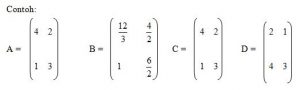
Dari contoh di atas matriks A = B = C
Tetapi C ≠ D sebab walaupun elemen-elemen kedua matriks sama, tetapi letak elemen-elemen itu berbeda, sehingga elemen-elemen yang bersesuaian tidak sama.
Transpos Suatu Matriks 
Dari matriks A dapat dibentuk matriks baru dengan cara elemen baris 1 matriks A ditulis menjadi elemen kolom 1 matriks baru, elemen baris 2 matriks A dijadikan kolom 2 matriks baru, dan seterusnya.
Matriks baru yang diperoleh disebut trans pos dari matriks A dan dinyatakan dengan AT (dibaca “trans pos A). baris-baris matriks A menjadi kolom-kolom matriks AT, dan kolom-kolom matriks A menjadi baris-baris AT.
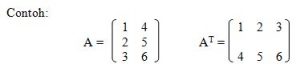
APLIKASI MATRIKS DI DUNIA NYATA 
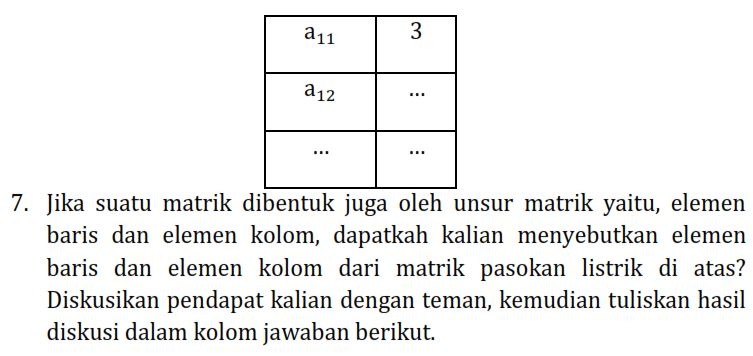
Dalam kehidupan sehari-hari banyak kita jumpai berbagai kejadian yang memiliki pola tertentu sehingga hal tersebut sangat membantu dalam aktivitas, salah satu contoh di showroom mobil. Dalam penataannya, pihak showroom mobil memajangkan mobil-mobil dengan berjejer rapih. Perhatikan gambar 1, salah satu showroom di Jakarta memajang mobil mobilnya di tiga tingkat lantai dan setiap tingkat lantai diberi tiga lapak mobil sedemikian sehingga setiap lapak hanya terisi oleh satu mobil. Apabila banyak tingkat lantai merepresentasikan baris dan banyak lapak setiap tingkat lantai merepresentasikan kolom, dapatkah kalian menyebutkan banyak baris dan kolom pada situasi tersebut?

Konsumen dengan mudah memilih mobil tersebut hanya dengan menyebutkan baris dan kolomnya. Misal, seorang konsumen ingin membeli mobil putih yang ada di lantai dua pojok kanan. Bagaiamana cara efektif menyebutkan menggunakan baris dan kolom? Baris, kolom dan unsur (elemen baris dan elemen kolom) merupakan pembentuk matriks. Contoh di atas merupakan matriks showroom, dimana setiap lantai dan setiap lapak hanya boleh diisi oleh satu mobil. Mobil sebanyak satu merepresentasikan elemen matriks. Artinya unsur matriks untuk baris kesatu dan kolom kesatu sebanyak 1, unsur matriks untuk baris kesatu dan kolom kedua sebanyak 1, dan seterusnya. Menurut kalian, bagaimana jika setiap lantai dan setiap lapak boleh diisi lebih dari satu mobil? Banyak sekali aplikasi dari matriks dalam kehidupan sehari-hari. Salah satu contoh penggunaan matriks adalah dalam mencari solusi sistem persamaan lanjar (SPL). Menurut Purba (2016) dalam bidang keilmuan yang mempelajari rangkaian listrik, tidak jarang digunakan matriks untuk menghitung besaran-besaran yang ada di dalamnya. Dalam bidang keilmuan elektro teknik , seperti teknik elektro, teknik tenaga listrik, maupun teknik telekomunikasi, rangkaian sederhana adalah dasar dari pembelajarannya. Rangkaian-rangkaian listrik yang kita jumpai selama ini menggunakan prinsip-prinsip yang ada pada hukum Kirchoff. Terdapat dua hukum Kirchoff yaitu hukum pertama Kirchoff atau KCL (arus) lalu hukum kedua Kirchoff atau KVL (tegangan). Dengan menerapkan kedua hukum tersebut akan didapatkan sebuah persamaan linear. Jika terdapat sebuah loop, maka hanya terdapat satu persamaan linear saja, namun jika ternyata terdapat banyak loop, maka persamaan linear yang dibentuk juga banyak sama seperti loop yang ada. Dengan banyaknya persamaan linear tersebut, mengakibatkan terbentuknya sistem persamaan linear (SPL). Dalam menyelesaikan sistem persamaan linear (SPL) terdapat banyak cara, cara yang paling umum yaitu subtitusi dan eliminasi. Untuk kasus SPL dua, tiga, dan empat variabel cara subtitusi dan eliminasi ini mungkin masih sangat efektif dan mudah. Namun bagaimana jika terdapat sistem persamaan linear dengan 10 variabel ? Cara tersebut memang bisa digunakan, namun waktu yang diperlukan untuk menyelesaikan realatif sangat lama, dan juga tingkat kesalahan yang didapatkan juga semakin besar.
Asah Kemampuan 1 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
1.Sebutkanlah ordo matriks berikut ini!
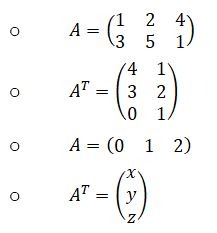
2.Berapakah banyaknya elemen setiap matriks pada soal nomor 1?
Tahukah kamu cara menghitung yang tepat?
3. Tuliskan sebuah contoh:
- Matriks 2 x 4
- Matriks 3 x 1
- Matriks 3 x 3
- Matriks 1 x 1
4.Tulislah transpos dari setiap matriks pada soal nomor 1 dan sebutkan
ordo setiap matriks transpos itu!

Penjumlahan dan Pengurangan Matriks 
Penjumlahan Matriks
Dua matriks A dan matriks B dapat dijumlahkan, jika ordo matriks A sama dengan ordo matriks B. Adapun caranya kita jumlahkan elemen matriks A dengan elemen matriks B yang bersesuaian letaknya (seletak).

Selanjutnya perhatikan contoh di bawah ini!

Karena P + Q = Q + P, maka penjumlahan matriks bersifat komotatif.

Dari contoh 2a dan 2b ternyata (A + B) + C = A + (B + C), maka pada penjumlahan matriks berlaku hukum assosiatif.

karena A + B = B + A = 0, maka setiap elemen B merupakan lawan atau negatif dari elemen A yang bersesuaian, sehingga matriks B disebut matriks negatife (lawan) A dan dinyatakan –A
Matriks nol adalah matriks yang semua elemennya nol dinyatakan dengan 0
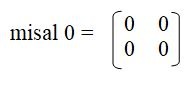
Pengurangan Matriks
Jika A dan B dua matriks yang ordonya sama maka matriks hasil pengurangan A dan B sama artinya dengan menjumlahkan matriks A dengan matriks lawan B.
Jadi A – B = A + (- B)
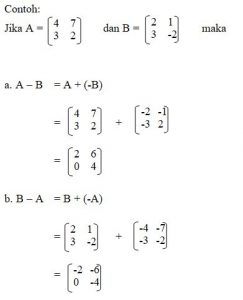
Karena A – B tidak sama dengan B – A maka pada pengurangan matriks tidak berlaku hukum homotatif.
Asah Kemampuan 2 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !


Perkalian Matriks 
Perkalian skalar (bilangan real) dengan matriks
Ide penjumlahan yang berlaku pada bilangan real dapat kita terapkan pada penjumlahan matriks, yaitu a + a = 2a, penjumlahan dua buah bilangan yang sama a + a + … + a = na, penjumlahan n buah bilangan yang sama.

Jadi A + A = 2A
Dengan demikian A + A + A = 3A
Dari uraian di atas dapat disimpulkan jika A adalah sebuah matriks dan k adalah skalar (bilangan real) maka k A adalah sebuah matriks baru yang didapat dari hasil perkalian k dengan elemen-elemen matriks A.
Perkalian Matriks dengan Matriks
Dua matriks dapat dikalikan, apabila banyaknya kolom matriks pertama sama dengan banyaknya baris matriks kedua.

Catatan:
Pemangkatan matriks berarti perkalian antara matriks itu sendiri, yaitu A2 = A.A;
A3 = A.A.A
= A2.A
Asah Kemampuan 3 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !


Invers Matriks Bujur Sangkar 
Jika A dan B adalah matriks bujur sangkar berordo sama sedemikian sehingga AB = BA = I. Maka B adalah invers A (B = A-1) dan A adalah invers B (A = B-1)

Sifat matriks satuan (I) menyerupai sifat-sifat satuan dalam bilangan real (1.A = A.I = A .A € R). Jika A adalah matriks ordo 2 maka I.A = A.I.A
Rumus Invers Matriks Bujur Sangkar Berordo 2 x 2

Catatan:
- Jika determinan (A) ≠ 0, maka A mempunyai invers dan disebut matriks nonsingular
- Jika determinan (A) = 0, maka A tidak mempunyai invers dan disebut matriks singular.


Determinan Matriks Ordo 3 x 3

Ada banyak cara untuk menghitung harga determinan matriks persegi ordo tiga. Antara lain dengan menggunakan aturan sarrus. Langkah-langkah menggunakan aturan sarrus adalah sebagai berikut:
- Letakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal dari determinan
- Jumlahkan hasil kali unsur-unsur yang terletak pada diagonal utama dengan hasil kali unsur-unsur yang sejajar dengan diagonal utama pada arah kanan, kemudian kurangi dengan hasil kali unsur-unsur yang terletak sejajar dengan diagonal samping.
Perhatikan skema berikut:

Adjoin Suatu Matriks
Sebelum kita membahas adjoin suatu matriks kita harus mengetahui terlebih dahulu minor dan kofaktor.
Missal A matriks bujur sangkar berordo 3 x 3, minor dari elemen aij matriks A adalah (Mij) dan kofaktor dari elemen aij = Aij adalah (-1)I + j (Mij).
Jadi, minor suatu elemen matriks adalah harga determinan dari elemen-elemen matriks dengan menghilangkan baris dan kolom yang memuat elemen tersebut.


Jika matriks A = (aij), dan kofaktor dari elemen aij kita sebut Aij, maka trans pos dari matriks (Aij) disebut adjoin dari matriks A.


Invers Matriks Bujur Sangkar Berordo 3 x 3
Dengan menggunakan matriks adjoin, maka kita dapat mencari inverts dari suatu matriks.
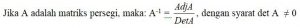

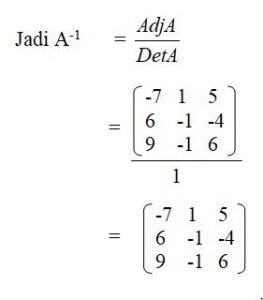
Asah Kemampuan 4 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !


Soal-soal UN Matriks 




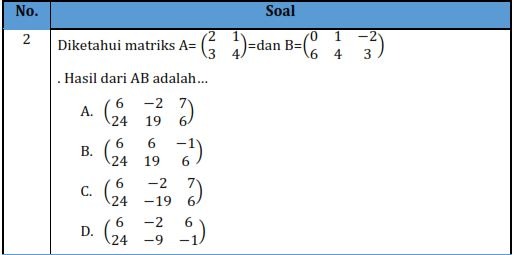









LKPD Pembelajaran HOTS 
LKPD 1







LKPD 2






LKPD 3






LKPD 4






LKPD 5





LKPD 6




![matriks [generasiemas2045.com]](https://www.generasiemas2045.com/wp-content/uploads/2020/08/matriks.jpg)

