Penjelasan logika matematika juga bisa melalui video di bawah ini !
Assalamu’alaikum Wr. Wb.
Selamat datang di Visi Pendidikan Generasi Emas 2045, terima kasih telah berkenan mampir di website saya generasiemas2045.com. Semoga Allah SWT senantiasa memberi kita kesehatan, keselamatan, perlindungan, kemudahan segala urusan dan rejeki untuk kita semua dan keluarga yang kita sayangi. Sholawat serta salam tidak lupa kita sampaikan pada beliau Nabi Muhammad SAW yang telah menuntun umat manusia dari zaman kegelapan menuju masyarakat yang tercerahkan.
Pada kesempatan kali ini, saya upload materi matematika dengan peta materi sebagai berikut :
Daftar Isi
- Pernyataan

- Asah Kemampuan 1

- Asah Kemampuan 2

- Ingkaran, Konjungsi, Disjungsi, Implikasi dan Biimplikasi

- Asah Kemampuan 3

- Asah Kemampuan 4

- Invers, Konvers, dan Kontraposisi

- Asah Kemampuan 5

- Penarikan Kesimpulan

- Asah Kemampuan 6

- Aplikasi Logika Matematika dalam Kehidupan

- Analisa Soal UN Logika Matematika

- LKPD Pembelajaran HOTS

LOGIKA MATEMATIKA
PERNYATAAN
Tujuan
Setelah mempelajari kegiatan belajar ini, anda diharapkan :
- Memiliki pemahaman tentang pengertian pernyataan dan bukan pernyataan
- Dapat memberikan contoh suatu kalimat pernyataan
- Dapat memberikan suatu contoh suatu kalimat yang bukan pernyataan
Uraian Materi 
Dalam Matematika, bahasa komunikasinya dinamakan kalimat matematika, yaitu kalimat yang menggunakan lambing-lambang matematika. Kalimat ini terbagi menjadi dua :
Kalimat yang bermakna
Kalimat yang bermakna adalah kalimat yang dapat ditarik suatu pengertian yang masuk akal dan berarti dalam fikiran.
Untuk lebih memahami perhatikan contoh berikut :
- Ani pergi ke pasar
- Pohon itu tinggi dan besar
- 5 lebih dari 3
Kalimat yang tidak bermakna
Kalimat yang tidak bermakna adalah suatu kalimat yang tidak dapat diterima akal. Untuk lebih memahami perhatikan contoh berikut ini :
- Siang hari belum nanti
- Tidak terbit gula gelap
Kalimat yang bermakna dibagi menjadi dua yaitu :
Kalimat pernyataan (statement)
Kalimat pernyataan adalah kalimat yang mempunyai nilai kebenaran, baik nilai kebenarannya benar atau nilai kebenarannya salah. Suatu kalimat mempunyai nilai benar jika yang dikatakan kalimat tersebut sesuai dengan keadaan yang sesungguhnya. Sedangkan suatu kalimat bernilai salah jika yang dikatakan dalam kalimat tidak sesuai dengan keadaan sesungguhnya. Nilai benar atau salah dari suatu pernyataan itulah yang disebut dengan nilai kebenaran.
Misalnya :
- Jakarta adalah ibukota negara Indonesia (Benar)
- 4 + 7 = 9 (salah)
Selain kalimat pernyataan bernilai benar atau salah, dikenal pula kalimat Faktual yaitu kalimat yang nilai kebenarannya belum tentu.
Perhatikan contoh kalimat berikut ini :
Hari ini cuaca cerah ( benar salahnya tergantung suasana pada saat dibicarakan ).
Kalimat bukan pernyataan
Kalimat bukan pernyataan adalah kalimat yang mempunyai arti, tetapi tidak mempunyai nilai benar atau salah. Yang termasuk dalam kalimat ini adalah kalimat terbuka, kalimat perintah, kalimat tanya dan kalimat harapan. Untuk lebih memahami perhatikan contoh berikut :
- 3x + 3 = 5
- Bersihkan lantai rumah kita !
- Mengapa kamu membolos kemarin ?
- x adalah biangan genap positif
Rangkuman
- Kalimat bermakna adalah kalimat yang dapat ditarik suatu pengertian yang masuk akal dan berarti dalam fikiran.
- Kalimat yang tidak bermakna adalah kalimat yang tidak dapat diterima akal.
- Kalimat pernyataan adalah kalimat yang mempunyai nilai kebenaran.
- Kalimat bukan pernyataan adalah kalimat yang mempunyai arti tetapi tidak mempunyai nilai kebenaran.
Asah Kemampuan 1 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Berilah contoh kalimat bermakna yang bukan suatu pernyataan (minimal 5).
- Berikan contoh kalimat tidak bermakna (minimal 5).
- Berikan contoh kalimat pernyataan (minimal 5).
- Berikan contoh kalimat bukan pernyataan (minimal 5).
Asah Kemampuan 2 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Manakah diantara kalimat berikut yang merupakan pernyataan ?
- Semua perusahaan besar milik konglomerat
- 236 habis dibagi 9
- Bintang itu bersinar terang
- Jumlah sudut dalam suatu segitiga adalah 180 derajat
- Kerjakan tugasmu hari ini dengan baik
- Tentukan benar atau salah pernyataan berikut !
- 2 + 5 = 7
- 3 adalah bilangan ganjil
- Matahari terbit dari barat
- Jakarta ada di Sumatra
INGKARAN, KONJUNGSI, DISJUNGSI, IMPLIKASI, DAN BIIMPLIKASI
Tujuan
Setelah mempelajari uraian kegiatan belajar ini, anda diharapkan :
- Dapat menuliskan Ingkaran, Konjungsi, Disjungsi, Implikasi dan Biimplikasi
- Menggunakan tabel kebenaran untuk menggunakan konjungsi, disjungsi, implikasi, dan biimplikasi
- Menerapkan masing – masing ingkaran, konjungsi, disjungsi, implikasi, dan biimplikasi dalam kalimat
- Dapat membedakan bukti langsung dan tak langsung
- Menentukan penarikan kesimpulan dari pembuktian
Uraian Materi 
Dua kalimat tunggal dapat dihubungkan satu sama lain adalah kata hubung logika ( logical connectives ), sehingga menjadi pernyataan majemuk (compoun statement).
Dalam logika matematika ada 5 macam kata hubung kalimat, yaitu:

INGKARAN / NEGASI
Ingkaran dari suatu pernyataan nilai kebenarannya berlawanan dengan nilai kebenaran kalimat semula. Notasi Ingkaran suatu pernyataan P ditulis ~p atau – p
Tabel Kebenaran
|
P |
~P |
|
B S |
S B |
Contoh:
1). p: 2 + 6 = 8 ( B )
~p : 2 + 6 ≠ 8 ( S )
~p : tidak benar bahwa 2 + 6 = 8 ( S )
2). p: manusia berjalan dengan perut ( S )
~p : manusia berjalan bukan dengan perut ( B )
~p : tidak benar bahwa manusia berjalan dengan perut ( B )
3). p : Semua siswa memakai seragam ( B )
~P : ada siswa yang tidak memakai seragam ( S )
~P : tidak benar bahwa semua siswa memakai seragam ( S )
KONJUNGSI
Suatu pernyataan p dan q dapat dibentuk menjadi pernyataan majemuk “ p dan q “ notasinya ditulis p ۸ q disebut konjungsi. Selain “ dan “ kata penghubung konjungsi yang lain adalah “meskipun, tetapi, sedangkan, yang, juga, walaupun. Konjungsi bernilai benar hanya jika kedua pernyataan tunggalnya bernilai benar .
Tabel Kebenaran
|
p |
q |
P ۸ q |
|
B B S S |
B S B S |
B S S S |
Contoh :
- p : SMK adalah sekolah kejuruan ( B )
q : 7 bilangan ganjil ( B )
p ۸ q : SMK adalah sekolah kejuruan dan 7 bilangan ganjil ( B )
- p : 2 + 3 = 5 ( B )
q : 2 + 3 > 7 ( S )
p ۸ q : 2 + 3 = 5 dan 2 + 3 > 7 ( S )
DISJUNGSI
Dua pernyataan p dan q dapat dibentuk menjadi pernyataan majemuk dengan kata hubung “ atau “ yang disebut disjungsi dari p dan q. Disjungsi “ p atau q “ dinotasikan dengan “ p V q “ . Disjungsi bernilai salah jika kedua pernyataan tunggalnya bernilai salah.
Tabel Kebenaran
|
p |
q |
P V q |
|
B B S S |
B S B S |
B B B S |
Contoh :
- p : 23 = 8 ( B )
q : 2 < 8 ( B )
p v q : 23 = 8 atau 2 < 8 (B)
- p : garam rasanya asin ( B )
q : madu rasanya pahit ( S )
p v q : garam rasanya asin atau madu rasanya pahit (B)
IMPLIKASI
Dua pernyataan p dan q dapat dibuat pernyataan majemuk “ jika p maka q “ yang ditulis dengan notasi “ p ⇒ q “ disebut implikasi atau kondisional .
- p disebut alasan / sebab /anteseden / hipotesis
- q disebut kesimpulan / akibat / konsekuen / konklusi
P ⇒ q dapat juga dibaca :
- p hanya jika q
- q jika p
- p syarat cukup bagi q
- q syarat perlu bagi p
Implikasi bernilai salah hanya jika antiseden bernilai benar dan konsekuen bernilai salah.
Tabel Kebenaran
|
p |
q |
P ⇒ q |
|
B B S S |
B S B S |
B S B B |
Contoh :
- p : 20 = 1 ( B )
q : log 1 = 0 ( B )
p ⇒ q : jika 20 = 1 maka log 1 = 0 ( B )
- p : London ibu kota kerajaan Inggris ( B )
q : Jakarta ibu kota Malaysia ( S )
p ⇒ q : Jika London ibukota kerajaan Inggris maka Jakarta ibukota
Malaysia ( S )
Implikasi yang berbentuk p(x) ⇒ q(x).
Jika P dan Q masing – masing merupakan himpunan penyelesaian dari kalimat terbuka p(x) dan q(x) pada himpunan semesta S, maka p ⇒ q benar jika P ⊂ Q.
Contoh :
- Jika x – 2 = 0 maka x2 = 4
p(x): x – 2 = 0 maka HP = P = {2}
q (x) : x2 – 4 = 0 maka HP = Q = {-2, 2}
Karena P ⊂ Q maka implikasi tersebut bernilai benar.
- Jika x bilangn prima maka x bilangan ganjil
P : himpunan bilangan prima
Q : himpunan bilangn ganjil
Karena P ⊄ Q maka Implikasi tersebut bernilai salah.
BIIMPLIKASI
Dua pernyataan p dan q dapat dibuat pernyataan majemuk “ p jika dan hanya jika q” yang ditulis dengan notasi “ p ⇔ q “ disebut biimplikasi / bikondisional / ekuivalen. Biimplikasi bernilai benar hanya jika kedua pernyataan tunggalnya bernilai sama (kedua pernyataan bernilai benar atau kedua pernyataan bernilai salah.
Dua pernyataan p dan q dapat dibuat pernyataan majemuk “ p jika dan hanya jika q” yang ditulis dengan notasi “ p ⇔ q “ disebut biimplikasi / bikondisional / ekuivalen. Biimplikasi bernilai benar hanya jika kedua pernyataan tunggalnya bernilai sama (kedua pernyataan bernilai benar atau kedua pernyataan bernilai sallah.
Tabel Kebenaran
|
P |
q |
P ⇔ q |
|
B B S S |
B S B S |
B S S B |
Contoh :
P : 2 adalah bilangn genap (B)
q : 3 adalah bilangn ganjil (B)
p ⇔ q : 2 adalah bilangan genap jika dan hanya jika 3 adalah bilangan ganjil.
Biimplikasi yang berbentuk p(x) ⇔ q(x).
Jika P dan Q masing – masing merupakan himpunan penyelesaian dari kalimat terbuka p(x) dan q(x) pada semesta pembicaraan S, maka p(x) ⇔ q(x) bernilai benar jika P = Q.
Contoh :
- x+2 = 0 jika dan hanya jika x2 – 4 = 0
p(x) : x+2 = 0 maka HP = P = {-2}
q(x) : x2 – 4 =0 maka HP = Q = { -2,2}
Karena p ≠ q maka biimplikasi tersebut bernilai salah.
- x ≥ -3 jika dan hanya jika 2x + 11 ≥ 5
p(x) : x ≥ -3 misalkan HP = P
q(x) : 2x + 11 ≥ 5
2x ≥ 5 – 11
2x ≥ -6
x ≥ -3 , misalkan HP = Q
Karena P = Q maka biimplikasi tersebut bernilai benar.
NILAI KEBENARAN PERNYATAAN MAJEMUK
Untuk menentukan nilai kebenaran pernyataan majemuk digunakan tabel kebenaran.
Contoh :
- Tentukan nilai kebenaran dari pernyataan majemuk ~ (p ۸ ~ q).
Jawab :
|
p |
q |
~q |
P ۸ ~ q |
~(p ۸ ~q) |
|
B B S S |
B S B S |
S B S B |
S B S S |
B S B B |
Jadi nilai kebenaran dari ~(p ۸ ~q) adalah B S B B
- Tentukan nilai kebenaran dari {(p⇒ q) ۸ p} ⇒ q
Jawab :
|
p |
q |
p ⇒ q |
(p⇒ q) ۸ p |
{(p⇒ q) ۸ p}⇒ q |
|
B B S S |
B S B S |
B S B B |
B S S S |
B B B B |
Jadi nilai kebenaran dari {(p⇒ q) ۸ p}⇒ q adalah B B B B
- Tentukan nilai kebenaran dari (p ۸ q) ۸ (~p V ~q).
Jawab :
|
P |
q |
~p |
~q |
P ۸ q |
~p V ~q |
(p ۸ q) ۸ (~pV ~q) |
|
B B S S |
B S B S |
S S B B |
S B S B |
B S S S |
S B B B |
S S S S |
Catatan :
- Pada contoh 1 nilai kebenaran pernyataan majemuk tersebut dapat bernilai benar atau salah maka pernyataan majemuk tersebut disebut
- Pernyataan majemuk yang selalu bernilai benar untuk semua kemungkinan nilai kebenaran dari pernyataan – pernyataan komponennya disebut Taotologi. Seperti pada contoh 2.
- Pernyataan majemuk yang selalu bernilai salah untuk semua kemungkinan nilai kebenaran dari pernyataan – pernyataan komponennya disebut Seperti pada contoh 3.
Tabel kebenaran dari pernyataan majemuk yang terdiri dari tiga pernyataan tunggal.
Contoh :
Tentukan nilai kebenaran dari pernyataan majemuk (p V q) ⇒ ~r
Jawab :
|
p |
q |
r |
~r |
p V q |
(p V q) ⇒ ~r |
|
B B B B S S S S |
B B S S B B S S |
B S B S B S B S |
S B S B S B S B |
B B B B B B S S |
S B S B S B B B |
Nilai kebenaran pernyataan majemuk (p V q) ⇒ ~r adalah S B S B S B B B
DUA BUAH PERNYATAAN MAJEMUK YANG EKUIVALEN
Dua buah pernyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk itu mempunyai nilai kebenaran yang sama untuk semua kemungkinan nilai kebenaran pernyataan – pernyataan penyusunnya.
Tautologi yang berbebentuk a ⇔ b dinamakan ekuivalen logis dan ditulis dengan lambang a Ξ b (dibaca a ekuivalen b).
Contoh 1 :
Buktikan bahwa (p ⇒ q) Ξ (~p V q)
Jawab :
|
q |
~p |
p |
p⇒ q |
~p V q |
|
B S B S |
S S B B |
B B S S |
B S B B |
B S B B |
Karena nilai kebenaran pÞq sama dengan nilai kebenaran ~ pVq maka (p⇒q) Ξ (~pVq).
Hukum De Morgan :
- ~ (p V q) Ξ (~p ۸ ~q) merupakan ingkaran dari disjungsi
- ~(p ۸ q) Ξ (~P V ~q) merupakan ingkaran dari konjungsi
- Ingkaran dari Implikasi : ~(p ⇒ q) Ξ p ۸ ~q
Contoh 2 :
Tentukan negasi dari pernyataan-pernyataan berikut ini
- Siswa kelas 1 rajin dan pandai
- 3 atau 5 bilangan ganjil
- Jika hari hujan maka angin bertiup kencang
- P ۸ ~q
- (p v q) ⇒ r
Jawab :
- Siswa kelas 1 tidak rajin atau tidak pandai.
- 3 dan 5 bukan bilangan ganjil
- Hari hujan tetapi angin tidak bertiup kencang
- ~p v ~(~q) Ξ ~p v q
- (p v q) ۸ ~ r
RANGKUMAN
- Notasi Ingkaran ~p atau –p
Tabel Kebenaran
|
P |
~P |
|
B S |
S B |
- Notasi konjungsi p ۸ q
Tabel Kebenaran
|
p |
q |
P ۸ q |
|
B B S S |
B S B S |
B S S S |
Konjungsi bernilai benar hanya jika kedua pernyataan bernilai benar.
- Notasi Disjungsi pvq
Tabel Kebenaran
|
p |
q |
P v q |
|
B B S S |
B S B S |
B B B S |
Disjungsi bernilai salah hanya jika kedua pernyataan bernilai salah
- Notasi Implikasi p⇒ q
Tabel Kebenaran
|
p |
q |
p ⇒ q |
|
B B S S |
B S B S |
B S B B |
Implikasi bernilai salah hanya jika anteseden bernilai benar dan konsekuen bernilai salah.
- Notasi Biimplikasi p ⇔ q
Tabel Kebenaran
|
p |
q |
p ⇔ q |
|
B B S S |
B S B S |
B S S B |
Biimplikasi bernilai benar hanya jika kedua pernyataan bernilai benar atau kedua pernyataan bernilai salah.
- Ingkaran dari konjungsi ~(p ۸ q) Ξ~p v ~q
- Ingkaran dari disjungsi ~(p v q) Ξ ~p ۸ ~q
- Ingkaran dari implikasi ~(p ⇒ q) Ξ p ۸ ~q
Asah Kemampuan 3 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Tentukan nilai kebenaran dari :
- Jika 5 x 5 = 10 maka 20 bilangan prima
- Semarang ibu kota Jawa Tengah atau Surakarta kota kabupaten
- Dolar mata uang Amerika jika dan hanya jika 25log x = -3, x = 5
- Semua bilangan genap habis dibagi 3 dan 15 bilangan prima
- Jika PR = PQ maka Δ PQR sama kaki
- ABCD belah ketupat jika dan hanya jika AC tegak lurus BD
- Jika 28 dan 30 habis dibagi 4 maka 7 atau 15 bilangan prima
- 23 = 8 atau 123 + 622 – 35 = 51267
- Tentukan ingkaran dari tiap pernyataan berikut ini :
- 2 adalah bilangan asli atau bilangan prima
- (-2)2 > (-2)3 dan –2 adalah bilangan negatif
- Jika harga barang naik maka permintaan turun
- Jika siswa rajin dan disiplin maka bapak atau ibu guru bangga
- Semua bilangan genap habis dibagi 3 dan 15 bilangan prima
- Jika PR = PQ maka Δ PQR sama kaki
- ABCD belah ketupat jika dan hanya jika AC tegak lurus BD
- Jika 28 dan 30 habis dibagi 4 maka 7 atau 15 bilangan prima
- 23 = 8 atau 123 + 622 – 35 = 51267
Asah Kemampuan 4 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Tulislah negasi atau ingkaran dari pernyataan dibawah ini :
- 2-0,5 > 20,5
- √2 bukan bilangan rasional
- (-3)5 merupakan bilangan negatif
- Bentuklah konjungsi dari pernyataan – pernyataan berikut ini, kemudian tentukan nilai kebenarannya
- p : 2 adalah bilangan genap
q : 2 adalah bilangan prima
-
- p : 2 x 3 = 2 + 3
q : 4,5 = 4 x 0,5
-
- p : es yang dipanaskan akan mencair
q : air adalah penghantar listrik
- Tentukan nilai kebenaran dari pernyataan berikut ini
- 6 adalah bilangan genap dan 7 > 8
- 5 dan 7 bukan bilangan prima
- Kambing adalah binatang menyusui atau harimau adalah binatang buas
- Tidak benar bahwa 32 = 10 atau 32 = 6
- Jika 5 adalah bilangan prima maka 5 = 2 x 3
- Jika setiap bilangan ganjil habis dibagi 2 maka setiap bilangan bulat habis dibagi 2
- Persamaan kuadrat mempunyai dua akar nyata yang berbeda jika dan hanya jika diskriminannya lebih dari nol
- Tentukan negasi dari pernyataan berikut ini
- 4 dan 3 adalah akar – akar persamaan kuadrat x2 – 7x + 12 = 0
- 2 bilangan genap atau 20 ≤ 3
- Jika x habis dibagi 6 maka x habis dibagi 2 atau 3
KONVERS, INVERS DAN KONTRA POSISI
TUJUAN
Setelah mempelajari uraian kegiatan belajar ini, anda diharapkan :
- Dapat menentukan invers dari suatu implikasi
- Dapat menentukan konvers dari suatu implikasi
- Dapat menentukan kontraposisi dari suatu implikasi
- Dapat menentukan nilai kebenaran pernyataan berkuantor
- Dapat menentukan negasi pernyataan berkuantor
URAIAN MATERI
INVERS, KONVERS DAN KONTRAPOSISI 
Dari suatu implikasi pÞ q dapat dibuat implikasi-implikasi baru, yaitu:
- Konvers : q ⇒ p
- Invers ~p ⇒ ~q
- Kontraposisi ~q ⇒ ~p
Untuk menentukan pernyataan – pernyataan yang ekuivalen, perhatikan tabel kebenaran dibawah ini :
|
p |
q |
~p |
~q |
p⇒ q |
q ⇒ p |
~p ⇒ ~q |
~q ⇒ ~p |
|
B B S S |
B S B S |
S S B B |
S B S B |
B S B B |
B B S B |
B B S B |
B S B B |
Dari tabel diatas diperoleh kesimpulan :
- Implikasi ekuivalen dengan kontraposisinya p ⇒ q Ξ ~q ⇒ ~p
- Konvers ekuivalen dengan invers q ⇒ p Ξ ~p ⇒ ~q
Contoh 1 :
Jika x > 3 maka x2 > 9
Konvers : Jika x2 > 9 maka x > 3
Invers : Jika x ≤ 3 maka x2 ≤ 9
Kontraposisi : Jika x2 ≤ 9 maka x ≤ 3
Contoh 2 :
Jika siswa rajin dan disiplin maka bapak atau ibu guru gembira
Konvers : Jika bapak atau ibu guru gembira maka siswa rajin dan disiplin
Invers : Jika siswa tidak rajin atau tidak disiplin maka bapak dan ibu guru tidak gembira
Kontraposisi : Jika bapak dan ibu guru tidak gembira maka siswa tidak rajin atau tidak disiplin
Contoh 3 :
( p ۸ q ) ⇒ ~ r
Konvers : ~ r ⇒ ( p ۸ q )
Invers : ~ ( p ۸ q ) ⇒ ~ (~ r) Ξ (~p v ~q) ⇒ r
Kontraposisi : r ⇒ (~p v ~q)
PERNYATAAN BERKUANTOR
Kuantor menyatakan kuantitas atau menyatakan “ berapa banyak “ yang ditunjukkan dengan kata “ semua “ atau “ setiap “, beberapa atau “ada”. Pernyataan berkuantor adalah pernyataan yang menggunakan kuantor. Ada dua macam kuantor yaitu kuantor universal dan kuantor eksistensial.
KUANTOR UNIVERSAL
Pernyataan berkuantor universal adalah pernyataan yang menggunakan kata “semua” atau “ setiap”. Notasi atau lambang kuantor universal adalah ∀. Sehingga pernyataan berkuantor universal dapat dilambangkan dengan (∀. x ) P(x) dibaca untuk “ semua x atau setiap x berlaku P(x) “ atau (∀. x ∈ S) P(x) dibaca untuk “ semua x atau setiap x anggota S berlaku P(x) “.
Nilai kebenaran (∀. x ) P(x) selain bergantung pada kalimat terbuka P(x) juga tergantung pada himpunan semesta.
Contoh 1 :
Semua bilangan genap habis dibagi 2
Pernyataan ini bernilai benar. Dapat juga dinyatakan dalam bentuk implikasi “ Jika x bilangan genap maka x habis dibagi 2 “
Contoh 2 :
(∀.x R) (x2 ≥ 0)
dibaca “ untuk semua x anggota himpunan bilangan real berlaku x2 lebih dari atau sama dengan nol . Pernyataan ini bernilai benar.
KUANTOR EKSISTENSIAL
Pernyataan berkuantor eksistensial adalah pernyataan yang menggunakan kata “beberapa” atau “ada”. Kata beberapa atau ada disini mengandung pengertian“satu atau lebih”, bisa juga diartikan “ sekurang-kurangnya satu “.Notasi atau lambang kuantor eksistensial adalah ∃ dibaca “beberapa” atau “ada” atau “ sebagian “. Sehingga pernyataan berkuantor eksistensial dapat dilambangkan dengan (∃x) P(x). Dibaca “ beberapa x berlaku P(x)” atau “ ada x berlaku P(x).
Contoh 1 :
Beberapa bilangan prima adalah bilangan genap.
Pernyataan ini bernilai benar, sebab 2 merupakan bilangan prima dan bilangan genap.
Contoh 2 :
(∃ x ∈ R) (2x + 1 ≥ 4)
Pernyataan ini bernilai benar, sebab dipenuhi untuk x≥ 1,5
Contoh 3 :
(∃ x ∈ R) (x2 +6 =0)
Pernyataan ini bernilai salah, sebab tidak ada bilangan nyata yang memenuhi. Kalimat terbuka dapat diubah menjadi pernyataan dengan menggunakan kuantor.
Contoh :
Kalimat terbuka : 3x + 2 = 6
Dengan kuantor universal : (∃ x ∈ R) (3x + 2 = 6) merupakan pernyataan yang bernilai salah.
Dengan kuantor eksistensial : (∃ x ∈ R) (3x + 2 = 6) merupakan pernyataan yang bernilai benar.
Untuk mengubah kalimat terbuka dengan dua variable sehingga menjadi suatu pernyataan diperlukan dua buah kuantor. Perhatikan definisi-definisi berikut ini :
- (∀ x) (∃ y) P (x,y) Ξ (∃ x) [ (∀ y) P (x,y) ] dibaca untuk setiap x terdapat y sehingga x dan y mempunyai sifat P
- (∃ y) (∀ x) P (x,y) Ξ (∃ y) [ (∀ y) P (x,y) ] dibaca terdapat y sehingga untuk setiap x, x dan y mempunyai sifat P.
- (∀ x) (∀ y) P(x.y) dibaca untuk setiap x dan setiap y,x dan y mempunyai sifat P
- (∃ x) (∃ y) P(x,y) dibaca ada x dan ada y sehingga x dan y berlakusifat P
Contoh :
Kalimat terbuka : 2x + 3y > 5 dapat dinyatakan sebagai pernyataan, diantaranya sebagai berikut :
- (∀ x E R) (y E R) (2x +3y > 5) pernyataan bernilai benar
- (∀ x E R) (∀ y E R) (2x +3y > 5) pernyataan bernilai salah
- (∃ x E R) (∃ y E R) (2x +3y > 5) pernyataan bernilai benar
NEGASI PERNYATAAN BERKUANTOR
NEGASI PERNYATAAN BERKUANTOR UNIVERSAL
Negasi dari pernyataan “semua siswa SMK gemar membaca” adalah “Tidak benar semua siswa SMK gemar membaca” berarti sekurang-kurangnya satu siswa SMK tidak gemar membaca, jadi dapat dinyatakan dengan “ada siswa SMK yang tidak gemar membaca”.
Dari contoh diatas dapat disimpulkan :
Negasi dari “semua x berlaku P(x)” adalah “ada (beberaPA) X tidak berlaku P(x)”. Jika dinyatakan dengan notasi : ~{(∀ x) P(x)} Ξ (∃ x)~ {P(x)}
Contoh :
1). Semua bilangan genap adalah bilangan rasional
negasi : beberapa bilangan bulat bukan bilangan rasional.
2). (∀ x ∈ R) (x2 > 0)
negasi : (x R) (x2 ≤ 0)
3). (∀ x ∈ R) (2x + 3 = 5)
negasi : (∃ x ∈ R) (2x + 3 ≠ 5)
NEGASI PERNYATAAN BERKUANTOR EKSISTENSIAL
Negasi dari pernyataan “ada siswa SMK yang malas” adalah “Tidak benar ada siswa SMK yang malas”,Pernyataan ini ekuivalen dengan “Semua siswa SMK tidak malas”.
Dari contoh diatas dapat disimpulkan :
Negasi dari “ada (beberapa) x berlaku P(x)” adalah “Semua x tidak berlaku P(x)”. Jika dinyatakan dengan notasi : ~{(∃ x) P(x)} Ξ (∀ x) ~ {P(x)}.
Contoh :
1). Beberapa bilangan genap habis dibagi 3
Negasi : Semua bilangan genap tidak habis dibagi 3
2). (∃ x ∈ R) (x – 2 ≤ 7)
Negasi : (∀ x ∈ R) (x – 2 > 7)
3). Ada siswa yang rajin dan disiplin
Negasi : Semua siswa tidak rajin atau tidak disiplin.
RANGKUMAN
- Dari implikasi p⇒q dapat dibuat implikasi baru yaitu :
Konvers : q ⇒ p
Invers : ~p ⇒ ~q
Kontraposisi : ~q ⇒ ~p
- Pernyataan berkuantor universal adalah pernyataan yang menggunakan kata semua atau setiap, Notasi kuantor universal adalah V.
- Pernyataan berkuantor eksistensial adalah pernyataan yang menggunakan kata beberapa atau ada. Notasi kuantor eksistensial adalah 3.
- Negasi pernyataan berkuantor universal : ~{(∀ x) P(x)} Ξ (∃ x)~ {P(x)}
- Negasi pernyataan berkuantor eksistensial : ~{(∃ x) P(x)} Ξ (∀ x) ~ {P(x)}.
Asah Kemampuan 5 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Tentukan konvers, invers dan kontraposisi dari implikasi berikut ini :
- Jika x > 0 maka x2 > 0
- Jika siswa tidak mengerjakan tugas maka guru marah
- Jika hari hujan maka Andre berteduh atau memakai paying.
- Jika adik malas dan nakal maka ayah atau ibu marah.
- Jika ada harga barang dan jasa naik maka semua orang resah.
- Tentukan negasi-negasi dari pernyataan-pernyataan berikut ini :
- Semua siswa mengikuti upacara.
- Ada bilangan genap yang tidak habis dibagi 4
- Semua siswa berpakaian seragam dan memakai sepatu.
- Beberapa bilangan nyata merupakan bilangan rasional atau bilangan irasional.
- Tentukan konvers, invers dan kontraposisi dari implikasi berikut ini :
- Jika x bilangan genap dan habis dibagi 3 maka x habis dibagi 6.
- Jika ada siswa yang tidak naik maka semua guru kecewa.
- Jika semua siswa naik atau lulus maka ada bapak dan ibu guru yang bangga.
- Tentukan nilai kebenaran pernyataan berkuantor berikut ini:
- Semua bilangan ganjil tidak habis dibagi 4
- Beberapa bilangan asli hanya mempunyai satu
- Ada bilangan bulat a sehingga a x 3 = 5
- Setiap segitiga sama kaki kedua sudutnya sama besar.
- Tentukan negasi pernyataan – pernyataan berikut ini :
- Semua bilangan prima adalah bilangan ganjil.
- Beberapa bilangan cacah tidak habis dibagi 5
- Semua bilangan bulat atau pecahan merupakan bilangan rasional.
- Beberapa guru dan semua siswa mengikuti seminar.
PENARIKAN KESIMPULAN
TUJUAN
Setelah mempelajari uraian kegiatan belajar ini anda diharapkan :
- Dapat menjelaskan pengertian modus ponens
- Dapat menjelaskan pengertian modus tollens.
- Dapat menjelaskan pengertian silogisme.
- Dapat membuktikan sah atau tidak suatu argumentasi.
URAIAN MATERI
PENARIKAN KESIMPULAN 
Salah satu penerapan logika adalah penarikan kesimpulan. Dari beberapa pernyataan yang diketahui bernilai benar ( disebut premis), dengan prinsip-prinsip logika dapat dibuktikan suatu pernyataan baru yang bernilai benar(disebut kesimpulan atau konklusi). Penarikan kesimpulan seperti ini disebut argumentasi. Argumentasi dikatakan sah atau berlaku yaitu jika semua premisnya benar maka konklusinya benar. Jika H adalah konjungsi dari semua premisnya dan K adalah konklusinya maka argumentasi sah jika implikasi H ⇒ K merupakan tautology (pernyataan yang selalu bernilai benar). Berikut ini akan dibahas 3 cara penarikan kesimpulan yaitu :
MODUS PONENS
Dari pernyataan-pernyataan p ⇒ q dan p yang bernilai benar dapat disimpulkan bahwa q benar. Penarikan kesimpulan dengan cara demikian disebut sebagai Modus ponens atau kidah pengasingan. Jika dinyatakan dalam simbul logika sebagai berikut :
Premis 1 : p ⇒ q
Premis 2 : p
Kesimpulan : q
Bukti : Cara 1
Premis 2 Kesimpulan Premis 1
|
p |
q |
p ⇒ q |
|
B |
B |
B |
|
B S S |
S B S |
S B B |
Pada baris pertama (bagian yang diarsir) tampak premis 1 yaitu p ⇒ q benar dan premis 2 yaitu p benar, maka konklusinya yaitu q juga bernilai benar, sehingga argumentasi tersebut sah.
Cara 2 :
Akan dibuktikan bahwa {( p ⇒ q) Λp} ⇒ q merupakan tautologi.
|
p |
q |
( p ⇒ q) |
(p⇒ q) Λ p |
{( p⇒ q) Λ p} ⇒ q |
|
B B S S |
B S B S |
B S B B |
B S S S |
B B B B |
Dari tabel tersebut terbukti {( p ⇒ q) Λ p } ⇒ q merupakan tautology, jadi argumentasi tersebut sah.
Contoh :
a). Jika x bilangan genap maka x habis dibagi 2
24 bilangan genap
Jadi 24 habis dibagi 2
b). Jika Gilang rajin belajar maka ia akan naik kelas
Gilang rajin belajar
Jadi Gilang naik kelas
MODUS TOLLENS
Dari pernyataan-pernyataan p ⇒ q dan~q yang bernilai benar dapat disimpulkan bahwa ~p benar. Penarikan kesimpulan dengan cara demikian disebut sebagai Modus Tollens atau Kaidah Penolakan Akibat.
Jika dinyatakan dengan notasi logika sebagai berikut :
Premis 1 : p ⇒ q
Premis 2 : ~q
Kesimpulan : ~p
Bukti : Cara 1
Premis 1 Premis 2 Kesimpulan
|
p |
q |
p ⇒ q |
~q |
~p |
|
B B S |
B S B |
B S B |
S B S |
S S B |
|
S |
S |
B |
B |
B |
Cara 2
Akan ditunjukkan bahwa { (p⇒ q) Λ ~q } ⇒ ~p merupakan tautology
|
p |
q |
~p |
~q |
p⇒ q |
(p⇒ q) Λ~q |
{ (p⇒ q) Λ ~q}⇒ ~p |
|
B B S S |
B S B S |
S S B B |
S B S B |
B S B B |
S S S B |
B B B B |
Contoh :
a). Jika Dido naik kelas maka ia gembira
Dido tidak gembira
Jadi Dido tidak naik kelas
b). Jika x habis dibagi 6 maka x habis dibagi 2 dan 3
17 tidak habis dibagi 2 atau 3
Jadi 17 tidak habis dibagi 6
SILOGISME
Dari pernyataan-pernyataan p ⇒ q dan q ⇒ r yang bernilai benar dapat disimpulkan bahwa p ⇒ r benar. Penarikan kesimpulan dengan cara demikian disebut Silogisme.
Jika dinyatakan dengan notasi logika sebagai berikut :
Premis 1 : p⇒ q
Premis 2 : q⇒ r
Kesimpulan : p⇒ r
Bukti :
Premis 1 Premis 2 Kesimpulan
|
P |
q |
r |
p⇒ q |
q⇒ r |
p⇒ r |
|
B |
B |
B |
B |
B |
B |
|
B B B |
B S S |
S B S |
B S S |
S B B |
S B S |
|
S |
B |
B |
B |
B |
B |
|
S |
B |
S |
B |
S |
B |
|
S |
S |
B |
B |
B |
B |
|
S |
S |
S |
B |
B |
B |
Pada baris-baris yang diarsir (baris ke-1, ke-5, ke-7 dan ke-8) premis 1 yaitu p⇒ q benar dan premis 2 yaitu q⇒ r benar, maka kesimpulannya yaitu pÞr juga bernilai benar.
Contoh :
a). Jika x habis dibagi 2 maka x bilangan genap
Jika x bikangan genap maka x2 genap
Jadi jika x habis dibagi 2 maka x2 genap.
b). Jika Dea rajin belajar maka ia dapat mengerjakan soal ujian.
Jika Dea dapat mengerjakan soal ujian maka ia lulus.
Jadi jika Dea rajin belajar maka ia lulus.
Sah atau tidak suatu argumentasi tidak tergantung pada benar atau tidak makna suatu kesimpulan sebagai pernyataan sebab ada argumentasi yang kesimpulannya bermakna wajar tetapi cara menarik kesimpulannya salah sehingga argumentasi tersebut tidak sah. Argumentasi yang demikian disebut kepalsuan.
Contoh :
Jika hari hujan maka pejalan kaki memakai payung
Pejalan kaki memakai payung
Jadi hari hujan
Kesimpulan itu mempunyai makna yang wajar tetapi tidak diperoleh dengan menggunakan prinsip-prinsip logika yang benar, sehingga argumentasi tersebut tidak sah.
Bukti :
Argumentasi tersebut dapat disusun dengan menggunakan lambang sebagai berikut :
p⇒ q
q
P
|
p |
q |
p⇒ q |
|
B |
B |
B |
|
B |
S |
S |
|
S |
B |
B |
|
S |
S |
B |
Pada baris ke 3 tampak, premis 1 yaitu p⇒ q benar dan premis 2 yaitu q benar tetapi kesimpulannya yaitu p bernilai salah.
Demikian juga ada argumentasi yang diperoleh dengan menggunakan prinsip-prinsip logika yang benar sehingga argumentasi tersebut sah tetapi kesimpulannya tampak tidak wajar. Hal ini bisa dikatakan ada premis yang tidak wajar.
Contoh :
Jika Andi lapar maka ia makan.
Jika Andi makan maka ia kenyang.
Jadi jika Andi lapar maka ia kenyang.
Argumentasi diatas berdasarkan kaidah silogisme, jadi kesimpulannya adalah sah, tetapi tampak tidak wajar karena premis 1 , belum tentu bernilai benar. Jadi kebenaran suatu kesimpulan ditentukan oleh kebenaran premis-premisnya.
RANGKUMAN
- Argumentasi adalah penarikan kesimpulan (konklusi) berdasarkan beberapa pernyataan yang diketahui bernilai benar yang disebut premis.
- Argumentasi dikatakan sah atau berlaku jika semua premisnya benar maka konklusinya benar
- Modus ponens atau kaidah pengasingan
Premis 1 : p⇒ q
Premis 2 : p
Kesimpulan : q
- Modus tollens atau kaidah penolakan akibat
Premis 1 : p⇒ q
Premis 2 : ~q
Kesimpulan : ~p
- Silogisme
Premis 1 : p⇒ q
Premis 2 : q⇒ r
Kesimpulan : p⇒ r
Asah Kemampuan 6 
Pelajari materi yang ada, Anda bisa mencari sumber lain juga sebagai referensi. Kerjakan soal di bawah ini !
- Buatlah masing-masing sebuah contoh penarikan kesimpulan modus ponens, modus tollens dan silogisme.
- Buktikan sah atau tidak sah argumentasi berikut ini :
- Jika hari hujan maka Tina memakai payung.
Tina tidak memakai payung atau Tina memakai mantel.
Jadi Jika hari hujan maka Tina memakai mantei.
- Jika hari hujan maka udara dingin.
Jika hari tidak hujan maka Gilang bermain diluar.
Jadi jika udara tidak dingin maka Gilang bermain diluar
- Jika gunung meletus atau banjir maka penduduk mengungsi.
Gunung tidak meletus tetapi banjir.
Jadi penduduk tidak mengungsi.
- Jika Anto lulus maka ia bekerja.
Jika Anto tidak beberja maka orang tuanya kecewa.
Jadi jika Anto tidak lulus maka orang tuanya kecewa.
- Tentukan kesimpulan yang dapat ditarik dari premis-premis berikut ini :
- Menggunakan modus ponens
Premis 1 : Jika dua garis sejajar maka kedua garis tersebut sebidang.
Premis 2 : Garis g sejajar garis h.
- Menggunakan modus tollens.
Premis 1 : Jika x2 > 4 maka x < -2 atau x > 2.
Premis 2 : -2 ≤ x ≤ 2
- Menggunakan silogisme
Premis 1 : Jika x ≥ 3 maka x2 ≥ 9
Premis 2 : Jika x2 ≥ 9 maka x2 + 1 ≥ 10.
- Buktikan sah atau tidak sah argumentasi berikut ini :
- Jika x sudut lancip maka cos x ≥ 0.
Sudut y tidak lancip
Jadi cos y < 0
- Jika x = 4 maka x2 = 16
Jika x = -4 maka x2 = 16
Jadi 4 = -4
- ~q ⇒ p
q V ~p
∴ q
Aplikasi Logika matematika dalam Kehidupan Nyata
Aplikasi pada Kehidupan Sehari-hari
Banyak fenomena atau istilah dalam kehidupan sehari-hari, baik langsung maupun tidak langsung, yang berkaitan dengan logika matematika. Gambar di bawah merupakan contoh pengumuman yang ditempel panitia bagi peserta suatu kegiatan yang akan melaporkan/mengumpulkan jawaban.

Dari kalimat pada gambar tersebut terlihat bahwa, peserta kegiatan dapat memilih salah satu media (atau bisa keduanya) untuk melaporkan/mengumpulkan tiket perjalanannya. Dengan tabel kebenaran (truth table) operasi logika ATAU (disjungsi), tiket perjalanan dapat diterima (bernilai BENAR) jika dikirim melalui e-mail, nomor WA, atau keduanya. Sebaliknya, (akan bernilai SALAH) jika tidak dikirim melalui keduanya. Begitu pula pada peraturan sekolah yang salah satunya mewajibkan siswa
mengenakan pakaian seragam dan sepatu cats ketika masuk ke sekolah. Dengan tabel kebenaran (truth table) operasi logika DAN (konjungsi), siswa dapat masuk ke sekolah (bernilai BENAR) jika mengenakan pakaian seragam dan sepatu cats (keduanya sekaligus). Sebaliknya, siswa tidak dapat masuk ke sekolah (akan bernilai SALAH) jika salah satu syarat tersebut tidak dipenuhi, apalagi keduanya.
Aplikasi pada Bidang Teknologi/Kejuruan di SMK
Penggunaan dan peran logika matematika dalam bidang teknologi/kejuruan di SMK relatif banyak dan bervariasi, terutama dalam bidang kelistrikan/elektronika, ilmu komputer, atau sistem digital.

Pada bidang kelistrikan/elektronika, prinsip dan operasi logika matematika digunakan dalam teori rangkaian atau saklar (switching theory). Terdapat dua jenis rangkaian dasar (SERI dan PARALEL) serta satu inverter. Dalam logika matematika, rangkaian SERI mempunyai prinsip dan operasi yang sama dengan konjungsi (DAN). Rangkaian PARALEL mempunyai prinsip dan operasi yang sama dengan disjungsi (ATAU). Sedangkan inverter mempunyai prinsip dan operasi yang sama dengan negasi/ingkaran (TIDAK/BUKAN). Pada ilmu komputer, prinsip dan operasi logika matematika digunakan dalam gerbang logika Boolean (logic gate). Terdapat dua operasi gerbang logika dasar (AND dan OR) serta satu inverter (NOT). Dalam logika matematika, operasi logika AND mempunyai prinsip dan operasi yang sama dengan disjungsi (DAN). Operasi logika OR mempunyai prinsip dan operasi yang sama dengan disjungsi (ATAU). Sedangkan inverter (NOT) mempunyai prinsip dan operasi yang sama dengan negasi/ingkaran (TIDAK/BUKAN).
Soal-soal UN Logika Matematika 












LKPD Pembelajaran HOTS
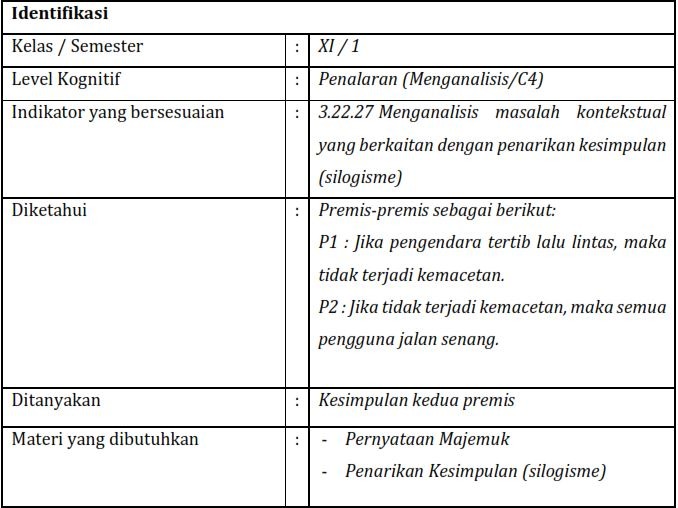
LKPD 1 



LKPD 2 














LKPD 3 




LKPD 4 






Materina lengkap
materi yang di berikan lengkap dan jelas
Terima kasih